Dropbox Paper

What makes blockchains secure? [5/5] (Final)

Discover & share this Hold GIF with everyone you know. GIPHY is how you search, share, discover, and create GIFs.

media.giphy.com

Animated GIF - Find & Share on GIPHY • media.giphy.com

In the past four posts, we have broadly covered the interaction between statistics and consensus. The first two posts aimed to give a bit of background about how to think about the analyses of consensus protocols from a probabilistic mindset. On the other hand, the latter two posts focused on trying to evince when there exist probabilistic equivalences between seemingly different protocols. In particular, the fourth post covered how one can classify protocols in a manner similar to how physical systems are classified. We argued that when two protocols are deemed not to be equivalent, there must exist a phase transition that makes a macroscopic observable (such as the expected Gini coefficient or average branching factor) have a discontinuous jump when we try to smoothly move from one protocol to the other [0]. For instance, Bitcoin will have a phase transition from block trees whose height is

\Omega(N)

, where

N

is the number of blocks produced, to block trees whose height is

\Omega(\log N)

(e.g. balanced trees), as we make the ratio of the block production rate to the network delay diameter smaller [1].

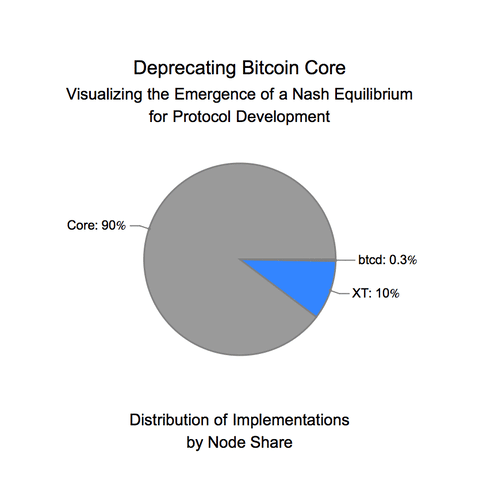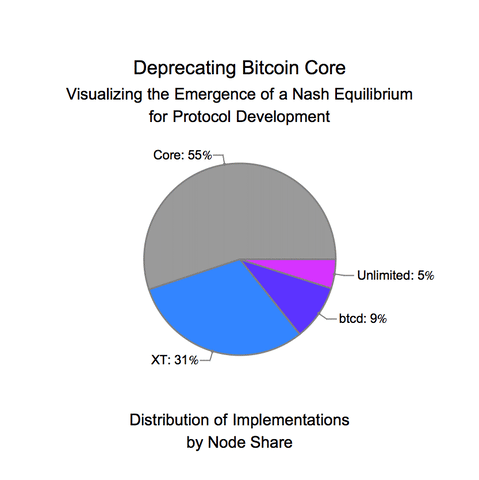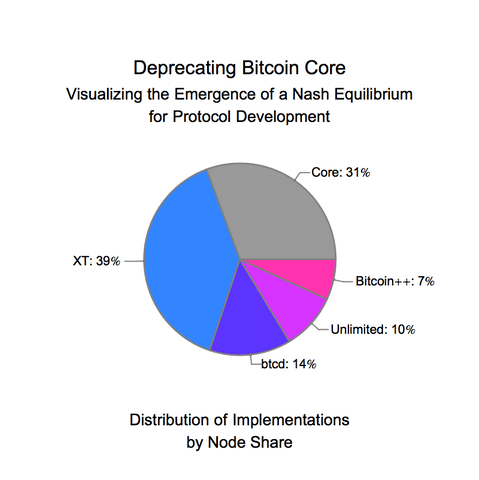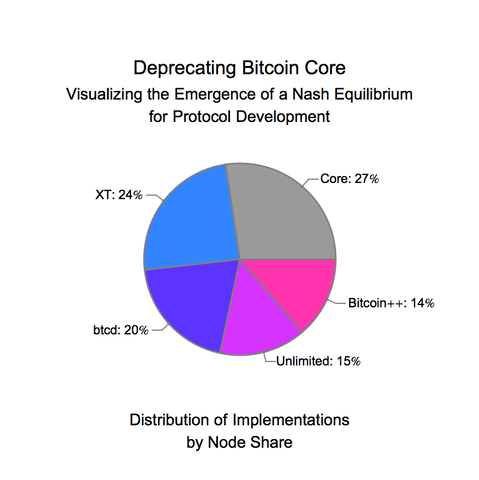
On the other hand, when blockchain protocols are in the wild, they appear to avoid crossing phase transition points. At a very coarse level, much of this empirical success is due to the formal Byzantine-resistance guarantees of the consensus protocol. However, reality has far more actors than those that are purely Byzantine and those that are purely honest, which means that the formal guarantees of a consensus protocol cannot fully describe practical implementations of consensus. This was most recently seen in Bitcoin with the Binance hack, where Binance’s CEO openly discussed bribing miners to revert a theft. The economics of a protocol — the block rewards, inflation rate, transaction fees, ease of speculation, access to leverage, existing liquidity — can dramatically affect the security of the protocol. This post will aim to illustrate that the game theory of the entire system — coupling both the consensus layer and the economic layer — works to keep the system away from phase transitions. Moving to a view that incorporates both layers dramatically changes the security and threat models and involves incorporating game theoretic considerations that can exponentially blow up the size of an environment [2].

As protocols increase in complexity and add in governance, maintenance of this probabilistic stability becomes increasingly important. For provenance, governance in cryptocurrencies refers to how the balance of power is split between the different users of a cryptocurrency. The simplest version of this power to change protocol behavior is split between developers (e.g. people contributing to the open source code base) and investors (e.g. people buying the tokens on an exchange). One of the main criticisms of Bitcoin and Ethereum is that they don’t admit governance. In Bitcoin and Ethereum, the authors of the code in the Bitcoin core and Ethereum client repositories completely dictate the economic and security decisions for the network. For Bitcoin, this has worked out well because Bitcoin aims to maximize security and minimize transaction complexity. In particular, Bitcoin is designed to not need governance, because its economics are meant to be non-malleable.

On the other hand, Ethereum has had a lot of issues with governance, such as the DAO hack and the Parity wallet hack. These issues affect people building on these platforms too — the controversy at stable lending platform MakerDAO has also led to questions about how much governance is needed within these systems. In MakerDAO, certain token holders vote on an analogue of interest rate of the system, which naturally affects token value. Some participants might want a larger interest rate (they are net lenders), whereas others might want a lower interest rate (they are net borrowers). Governance allows for the system to continuously vote on these types of parameters and reward people for voting / positive participation. These votes, however, can cause dramatic changes to stability and agent composition, which add protocol turmoil. A lot of governance issues come from the increased complexity of trying to build the ‘world computer’ as opposed to a simple transaction mechanism. Still, the idea that a community can develop an economic system that forces protocols to avoid phase transitions and is invariant to perturbations of agent types to stay within a universality class is fascinating in its own right.

In order to understand how to correctly model the entire ecosystem around a protocol or contract, we will need to figure out which statistical and empirical tools best apply to crypto networks. Our goal is to find a natural definition of economic equilibrium that meets the computational, adversarial, and statistical constraints that exist within crypto networks. We will begin by exploring other attempts to quantify adversarial behavior in distributed and multi-agent systems. First, we will briefly look at the history of algorithmic game theory and describe the different equilibria that are studied in this field. These equilibria will turn out to be too difficult for realistic users of crypto networks to compute, which will lead us to explore easier-to-compute equilibria that are studied in the field of Systems Engineering. Unfortunately, these equilibria will turn out to have other flaws regarding their interpretability and robustness. We will conclude by exploring Agent-Based Modeling, which aims to provide empirically computable and interpretable equilibrium estimates. I hope that this voyage through computation, game theory, and statistics will convince you of both the beauty and necessity of simulation within the study of crypto networks.

Multi-agent systems have been quantitatively studied in earnest for the past 75 years. The first attempts at quantitatively describing such systems began with Daniel Bernoulli’s 18th century explorations into games of chance. He was the first to describe the probabilistic concept of a martingale, which expressed how to compute conditional expectations in games of chance, such as coin-flipping in the St. Petersburg Paradox. These games of chance represented simple betting games that were common in Europe (and in particular, France) at that time. However, this inquiry into the nature of purely random games ignores what happens when agents can learn and adapt their strategies. Strategies, like much of early economics, were defined in terms of an agent’s preferences for different outcomes that arose executing a strategy on a certain state. For instance, an poker-playing agent might strongly prefer to fold when their maximum card is a 5 and they have no repeated cards. In order to express strategies via an agent's preferences over a set of possible actions, we need a way of mathematically expressing an agent’s preferences. There are two ways that people have historically done this:

Ordinality: There is a non-random ordering or preference among actions that a player can take when the game is in a certain state

Cardinality: There are strict relative preferences between every pair of actions that a player can take

Ordinal preferences are easier to study, as one can reduce the problem of picking an optimal strategy to elementary combinatorics. However, ordinality doesn’t allow for a game analyst to compare the difference of payoff magnitudes between two competing strategies. For instance, suppose that I know that one poker hand is better than another, but I don’t know how much it increases my chance of winning. Would this really be useful for poker strategy development? On the other hand, cardinal preferences convey information about payoff magnitudes but introduce a variety of analytic considerations and non-convexity that make analyses difficult. Cardinal preferences are represented by a utility function, which maps states to the real line which provides an ordering and a magnitude.

Behavioral studies have shown that humans tend to reason about the world via ordinal preferences — after all, you don’t choose between two items that are priced the same via price alone. It was only in the 20th century that mathematicians invented general formalisms could convert strategies dependent on ordinal preferences to ones dependent on cardinal preferences. This formalism allowed for rigorous strategy development for games. This formalism’s main results from the 1940s, the von Neumann-Morgenstern theorem and the minimax theorem, set off an explosion of study into the mathematical foundations of what we now call game theory. By the end of that decade, economists had a formal definition of equilibrium for a system of agents — when an agent, conditional on all other agent’s preferences, cannot improve their utility by switching to a more preferred state — and John Nash had proved the existence of this equilibrium for all finite player games with a finite number of pure strategies [3]. At this point, mathematicians (especially real analysts) began to flood into economics and flesh out the expanse of game theory.

However, most of the improvements from the ‘50s to the ‘80s did not come from a deeper theoretical understanding of the agent-based model that Nash and von Neumann worked with. Instead, many of the developments within game theory, such as the existence of Bayes-Nash equilibrium, the description of coordinated games and Schelling points, and various ‘impossibility of equilibrium’ results came from better models and an improved understanding where impossibility theorems would arise. The Stanford Encyclopedia of Philosophy has an amazing article on the history of game theory that chronicles the epistemological evolution of game theory and the theoretical hurdles that were met as game theorists tried to make models more realistic. An understanding of why there were so many impossibility results only came in the ’90s, when theoretical computer scientists tried to ask the questions, ‘how complex is it to compute a Nash equilibrium?’

Gödel prize winner Christos Papadimitrou proved that a new complexity class, PPAD, was necessary to describe the complexity of computing Nash Equilibria. This was done by extending a known pivoting algorithm called the Lemke-Howson algorithm [4] to a more generic class of algorithms for finding fixed points [5]. These complexity results, coupled with a spate of examples of empirically observed market equilibria that did not fit into the mold of Nash Equilibria, suggested that humans interacting with games and institutions find different, less complicated equilibria. The empirical market success of the second price auction (and it's generalizations) at Google and Facebook hinted that simplicity is preferred to precision when it comes to observable equilibria. As such, the tools of algorithmic game theory alone will not suffice for describing crypto network equilibria and we will explore another avenue: Systems Engineering.

User-uploaded image: Complexity-classes-studied-in-this-survey-In-a-NE-stands-for-Nash-equilibria-In.png

Best guess at the set hierarchy for the complexity classes P, PLS, PPAD, TFNP, NP

In tandem with the high brow game theoretic results of the late 20th century was the development of the mathematically pedestrian yet pragmatic field of Systems Engineering (SE). This field, whose genesis was spurned by the complex systems pariah of electrical engineering, mathematics, mechanical engineering, and physics departments, aimed to find the simplest explanations for complex phenomena. At its best, the field produces novel, falsifiable syntheses of heuristics and insights from many fields, exemplified by research at places like the Santa Fe Institute. On the other hand, the field is also notable for producing a number of non-falsifiable, “not even wrong” results that get used in production to the tune of disaster (this paper details a number of examples of this). The extremely simplicity of the models (think: simple harmonic oscillators) used often can get some qualitative phenomena correct, but miss critical points and phase transitions that are where adversarial conditions lie. An explicit example of this can be found in the following Wired article. The article goes through an incident where GM had an order of magnitude increase in the failure rate of a critical component because they used a simple model to estimate the melting point of a complex material. This simple model dramatically misestimated when a phase transition due to overheating would occur and this caused a dramatic spike in the failure rate of their part. Their simple model, when compared to the Vextec finite-element model that is described in the article, provides an example of what happens when models that need to accurately represent phase transitions are underspecified.

A SE perspective on crypto networks (in the guise of differential games [6]) would likely start by taking a simple model of agent behavior, such as representing an agent’s utility function by an oscillator, and asking what happens if we deterministically combine

N

of these simple models. This provides a natural evolution operator, the Hamiltonian, for evolving the state of the all actors in the system. The SE literature usually refers to the combination of a state evolution operator and (potentially non-convex) constraints as a “generalized state space model.” The upshot of doing this analysis is that natural correlation lengths and time scales can be analytically computed or estimated to high precision. In this context, a “length” scale can refer to a physical length — a physical or graph distance between validators — or an abstract distance, such as a non-Euclidean distance between oscillator parameters [7]. These length and time scales help parametrize how stable the system is as

N

varies and give intuition as to whether a protocol configuration is “at the top of a hill” (unstable equilibrium) or “in the bottom of a valley” (stable equilibrium). This notion of equilibrium is easy to compute and the associated length and time scales provide intuitive conditions for when the system is at equilibrium. For instance, Bitcoin is at a stable equilibrium when the ratio of block production rate to delay diameter is greater than a constant, which couples a time scale (block production rate) to a distance measure (delay diameter) [8].

Unfortunately, these equilibrium scales and other scaling exponents (such as Lyapunov exponents) are usually presented in a way that is hard to correlate with real data. Moreover, they are statistically difficult to measure as a realistic crypto network is unlikely to cleanly fit into the mold of such state space models because of two qualities: adversarial agents and heteroskedastic, non-stationary data. In [9], I give a precise mathematical example of how adversarial agents can exponentially decay the statistical quality of a correlation length or exponent in an SE model by using random adversaries. An adversary that has any capacity to learn would do much better than this example, which illustrates how weak these types of models are for describing realistic crypto network agents. We note that there has been some work in the blockchain space that attempts to apply these techniques without considering these pitfalls, rendering their results statistically useless.

This dialectic story of game theory and SE naturally begs the following question: How can we get the best of both worlds? Can we get the rigor and statistical fortitude of game theoretic results while preserving the simplicity and intuition of methods from Systems Engineering? I believe that the only way to do this is via Agent-Based Modeling.

Agent-Based Modeling (ABM) aims to construct all of the different actors in a complex system via models that make statistics transparent and convergence rates interpretable. ABM is most useful when one is dealing with a system where it is hard to understand the effect of a certain policy and the cost of experimentation is high. By imbuing an ABM framework with realistic models of adversaries and semi-adversaries, and by utilizing real-world data, we argue that the results from ABM should reflect reality. It is most commonly used when backtesting algorithmic trading strategies via simulation — one models their strategy as an agent and other agents in the market (e.g. TWAP engines) and has them play a game against historical market data. This output of this simulation is then used to construct an objective function that can be used for optimizing a strategy. The usage of simulation allows for a strategy developer to avoid costly losses in live trading by stress testing against historical data and other actors in the system. Moreover, it lets the developer test against hard to realize edge cases (e.g. the flash crash) and search a larger portion of the strategy space. However, agent-based modeling has been used in a variety of contexts, including but not limited to: artificial intelligence, autonomous vehicles, cybersecurity, economics, and self-driving cars. Recently, there have been a variety of prominent empirical successes in the field including (but are not limited to):

Go: AlphaGo / AlphaGo Zero

StarCraft: AlphaStar

Online Poker: Libratus

Noam Brown and Tuomas Sandholm came up with an ingenious way of nesting subgames and solving for ‘local Nash’ that beat the best humans at online poker. This methodology is unique because it was a) debuted at NIPS 2017 b) doesn’t use deep learning and c) is extremely simple

The theoretical and empirical study of agent-based models resembles the construction of environments from the second blog post in this series, where we create an idealized simulation that does the following:

Instantiate $N$ agents from $T$ different agent classes

Instantiate an oracle that governs how they are allowed to interact with one another

For some number of rounds:

The oracle randomly selects a subset of agents

The selected agents are allowed to utilize bounded compute resources [10a] to evaluate a utility or value function based on global/public and local/private data

This allows them to take an action

The oracle propagates that action to the rest of the players